The first thing we have to do is come up with a metric of success when evaluating "how good" a particular draft pick is. Unfortunately, basketball doesn't have something like baseball's near-perfect WAR (Wins Above Replacement), which attempts to boil down everything a player does into one convenient number. ESPN's Real Plus-Minus is in my opinion basketball's closest equivalent, albeit it has flaws, namely its equal weighting of every single point scored, even those in "garbage time;" also, the metric only dates back to 2013, not nearly far back enough for the scope of this project. At the end of the day we settled on "Win Shares Per 48 Minutes" (WS/48). What win shares attempts to do is figure out how much each player contributed to their team's win total. For example, take the Warriors last year, who had 67 regular season wins. You'd expect, correctly, that Stephen Curry and Kevin Durant might be credited with a considerable portion of those wins; their win shares register at 12.6 and 12.0 respectively for last season. On the other hand, James Michael McAdoo's win shares registers at 1.1. The "per 48 minutes" part standardizes the statistic across different playing times: Stephen Curry's WS/48 for 2016-17 is 0.229, McAdoo's is 0.117, while Kevin Durant's is 0.278 -- higher than Curry's because he played 17 fewer games (and thus much fewer minutes) than his teammate due to injury. So what we are doing to assess how good a player was for his career is to take the career average of his WS/48 that Basketball-Reference gives. I'll freely admit a few flaws with this approach:
(if you're on a mobile phone right now, turn it sideways/landscape to view the following, and scroll on the left where the Y-axis is labeled)
(if you're on a mobile phone right now, turn it sideways/landscape to view the following, and scroll on the left where the Y-axis is labeled)
(above: in case you were curious about a "comparable comparison" of career-averages versus by-season data)
1. Could unfairly hurt players who played well into their 30's compared to those who retired shortly after their primes, as the lower win share seasons towards the end of the former’s career can drag down the player's career WS/48 average, if you follow.
2. The same sort of phenomenon applies to recent draftees. They could easily be hurt more -- relative to guys who have played out their entire careers -- given the "career average" aspect of our WS/48, as the recent draftees have only played the first couple years of their career. This hurts these youngsters because they have yet to develop towards their full potentials, and thus quite likely have not had their best win share seasons.
3. As well, the "win shares" aspect has been criticized by some people who argue that if, say, James Michael McAdoo were on the Nets instead of the Warriors but had performed exactly as well, he would have had much less win shares simply due to the fact that there's a smaller pie to take a portion of. However, “win shares enthusiasts” counter that although there’s a smaller pie in Brooklyn compared to that of Golden State, McAdoo would have had a larger portion of it as a Net, and thus all would have evened out. Since McAdoo unfortunately does not have a perfect clone on the Nets for us to compare him to, we don’t really know who’s right.
4. And of course, "per 48 minutes" has been criticized as well. While it does correct for some unfairness (Durant being injured as given in the example above, as well as players unjustly being used by the coach much less than they should be), the minutes standardization might give an undue bonus to guys who are effective in only five minutes or so per game -- could they keep up that same level of productivity over a 36-minute-per-game workload? Unlikely, and that's where fatigue-related factors that the "per 48 minutes" standardization fails to account for come in.
But with all that being said, Win Shares per 48 Minutes is still an excellent metric, even with the unfair career averages that we are taking, and gives us a very good sense of how good a player has been with only one number. If you would like to read more about the statistic, click here to read Basketball-Reference's article describing it, and here if you're curious about how it ranks players all-time. Anyways, moving on then.
So we decided to take data on every draft pick selected from 1 to 30, from 1985 to 2015, and...
"Hold on, how'd you choose those numbers?"
Fine, if you insist.
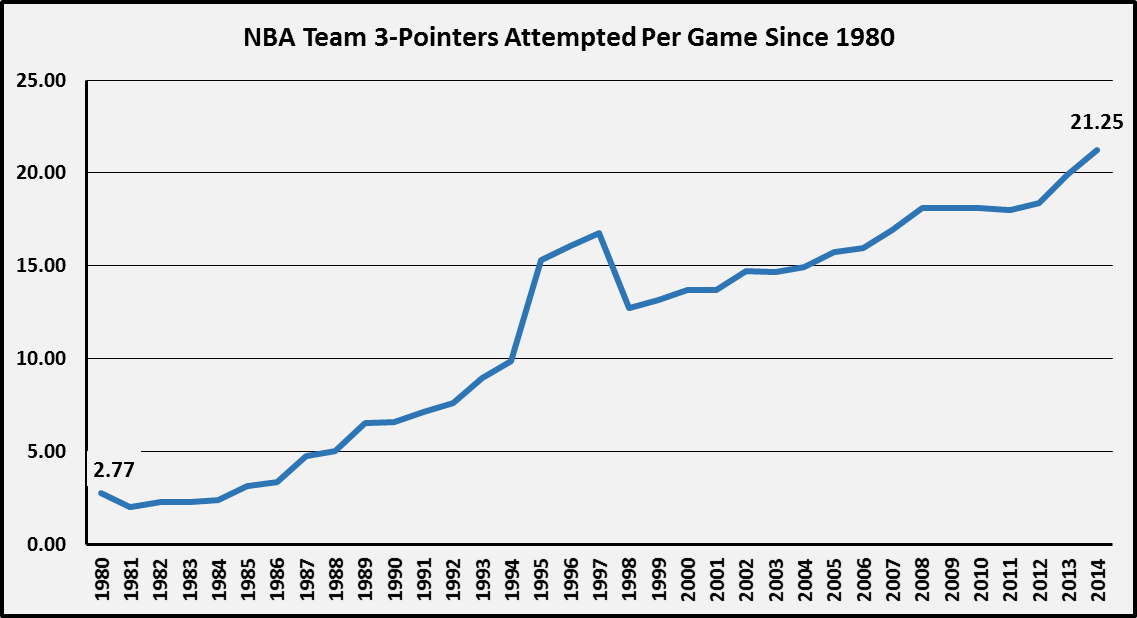
1985 was chosen as the cutoff date for semi-arbitrary, but defensible, reasons. It wasn't until the 1970's were through that blocks, steals, turnovers, and threes had all been added to basketball and its box scores, so we couldn't go much further back in that regard without these vital statistics. As well, 1985 was when the lottery era began, and it was only four years later did the draft drop to two rounds (prior, you saw MLB-esque drafts). Furthermore, have a look at this chart:
1. Could unfairly hurt players who played well into their 30's compared to those who retired shortly after their primes, as the lower win share seasons towards the end of the former’s career can drag down the player's career WS/48 average, if you follow.
2. The same sort of phenomenon applies to recent draftees. They could easily be hurt more -- relative to guys who have played out their entire careers -- given the "career average" aspect of our WS/48, as the recent draftees have only played the first couple years of their career. This hurts these youngsters because they have yet to develop towards their full potentials, and thus quite likely have not had their best win share seasons.
3. As well, the "win shares" aspect has been criticized by some people who argue that if, say, James Michael McAdoo were on the Nets instead of the Warriors but had performed exactly as well, he would have had much less win shares simply due to the fact that there's a smaller pie to take a portion of. However, “win shares enthusiasts” counter that although there’s a smaller pie in Brooklyn compared to that of Golden State, McAdoo would have had a larger portion of it as a Net, and thus all would have evened out. Since McAdoo unfortunately does not have a perfect clone on the Nets for us to compare him to, we don’t really know who’s right.
4. And of course, "per 48 minutes" has been criticized as well. While it does correct for some unfairness (Durant being injured as given in the example above, as well as players unjustly being used by the coach much less than they should be), the minutes standardization might give an undue bonus to guys who are effective in only five minutes or so per game -- could they keep up that same level of productivity over a 36-minute-per-game workload? Unlikely, and that's where fatigue-related factors that the "per 48 minutes" standardization fails to account for come in.
But with all that being said, Win Shares per 48 Minutes is still an excellent metric, even with the unfair career averages that we are taking, and gives us a very good sense of how good a player has been with only one number. If you would like to read more about the statistic, click here to read Basketball-Reference's article describing it, and here if you're curious about how it ranks players all-time. Anyways, moving on then.
So we decided to take data on every draft pick selected from 1 to 30, from 1985 to 2015, and...
"Hold on, how'd you choose those numbers?"
Fine, if you insist.
1985 was chosen as the cutoff date for semi-arbitrary, but defensible, reasons. It wasn't until the 1970's were through that blocks, steals, turnovers, and threes had all been added to basketball and its box scores, so we couldn't go much further back in that regard without these vital statistics. As well, 1985 was when the lottery era began, and it was only four years later did the draft drop to two rounds (prior, you saw MLB-esque drafts). Furthermore, have a look at this chart:
There is a pretty steady upward trend here, other than the spike in the mid-90s where the three-point line was actually temporarily moved in (little-known fact!). But at the end of the day when choosing the cutoff date (which has to be some year), we just felt that we wanted to get as much data as possible, while still comparing players who played the same game, so to speak. But a guy who spends his whole career on a team that takes less than five threes per game, compared to the Rockets taking over 40 long-range attempts per game nowadays? Well, those two sports are just unrecognizable. Thus 1985 hath been (arbitrarily) decided upon. Carry on.
So what's the plan? How are we going to evaluate how well teams selected players with the picks they had?
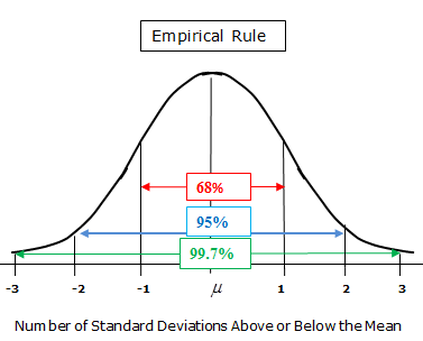
Well so each draft slot must get a mean and a standard deviation (describes the spread of a data set) of their Win Shares per 48 Minutes. For example, draft slot #1 (encompassing all #1 picks from 1985-2015) has a mean of about 0.134 WS/48 and a standard deviation of about 0.06. David Robinson, tied for the best player in our data set with Chris Paul (who is a #4 pick) at 0.250 WS/48 (1985 is the year after MJ was drafted, excluding him from the data), is 1.92 "standard deviations above the mean" (0.06x + 0.134 = 0.250 ... x = 1.92), thus giving him a "z-score" of +1.92. Infamous bust Michael Olowokandi, on the other hand, the number one pick in 1998, has a career WS/48 that barely registers at merely 0.009, or -2.07 "standard deviations above the mean" (0.06x + 0.134 = 0.009 ... x = -2.07). Thus Olowokandi's "z-score" as a number one pick is negative 2.07. Follow? Good.
Thus the idea here is to determine every player's z-score, and add them all up -- positive and negative -- by team (ex: Spurs get a nice bonus from Robinson, Clippers are hurt by the Olowokandi selection) and take all of the sums and create a ranking system that way. Only we realized that there was one serious flaw with that methodology…
So what's the plan? How are we going to evaluate how well teams selected players with the picks they had?
Well so each draft slot must get a mean and a standard deviation (describes the spread of a data set) of their Win Shares per 48 Minutes. For example, draft slot #1 (encompassing all #1 picks from 1985-2015) has a mean of about 0.134 WS/48 and a standard deviation of about 0.06. David Robinson, tied for the best player in our data set with Chris Paul (who is a #4 pick) at 0.250 WS/48 (1985 is the year after MJ was drafted, excluding him from the data), is 1.92 "standard deviations above the mean" (0.06x + 0.134 = 0.250 ... x = 1.92), thus giving him a "z-score" of +1.92. Infamous bust Michael Olowokandi, on the other hand, the number one pick in 1998, has a career WS/48 that barely registers at merely 0.009, or -2.07 "standard deviations above the mean" (0.06x + 0.134 = 0.009 ... x = -2.07). Thus Olowokandi's "z-score" as a number one pick is negative 2.07. Follow? Good.
Thus the idea here is to determine every player's z-score, and add them all up -- positive and negative -- by team (ex: Spurs get a nice bonus from Robinson, Clippers are hurt by the Olowokandi selection) and take all of the sums and create a ranking system that way. Only we realized that there was one serious flaw with that methodology…

 RSS Feed
RSS Feed